Lazy Model Expansion:
Interleaving Grounding With Search

Broes de Cat, Marc Denecker, Peter J. Stuckey,
Maurice Bruynooghe, Bart Bogaerts

FO(ID)

Typed first-order logic
Inductive Definitions

Running Example: Sokoban

\[ \begin{array}{l} \left\{\begin{array}{l} \forall o, p: At(o,p,0)\leftarrow At_{in}(o,p)\\ \forall o, p, t: At(o, p ,t+1) \leftarrow Goto(o,p,t)\\ \forall o, p, t: At(o, p ,t+1) \leftarrow At(o,p,t) \land \lnot \exists p': Goto(o,p',t)\\ \end{array}\right\}\\ \left\{\begin{array}{l} \forall p, t: Goto(Sok,p,t) \leftarrow Move(p,t)\\ \forall b[Block], p, t: Goto(b,p,t) \leftarrow Push(b,p,t)\\ \forall b,p,p',t: Push(b,Next(p,p'),t) \\ \quad \leftarrow At(Sok,p,t) \wedge At(b,p',t)\wedge Move(p',t)\\ \end{array}\right\}\\ \forall p, t: Goto(p,t)\Rightarrow Empty(p,t) \vee \exists b[Block]: At(b,p,t)\\ \forall b, p, t: Push(b,p,t) \Rightarrow Empty(p,t)\\ \forall p, t: Empty(p,t) \Leftrightarrow \lnot \exists o: At(o,p,t)\\ \forall o, t: AtGoal(o,t) \Leftrightarrow At(o,Goal(o),t)\\ \forall t: GoalReached(t) \Leftrightarrow: \forall o: AtGoal(o,t) \end{array} \]

Model Expansion

Input: 
  • theory T
  • partial interpretation S 
  • (output)vocabulary V

Output:
V-structure(s) M such that there is a M'
  • M' is a model of T
  • M' is more precise than S

Planning Problems

Output: actions

Scheduling Problems

Output: schedule

Model Expansion: How?

First: ground to ECNF (extended CNF)
Then: solve the ground problem

Problems

  • Large domains
  • Many nested quantifiers
  • Infinite domains: impossible

Solution

Don't make the entire grounding
Only ground what is necessary

Lazy Grounding

Ground parts of the theory
based on the state of the solver

Lazy Grounding: How

Some examples

Universal Quantifications

$\forall b, p, t: Push(b,p,t) \Rightarrow Empty(p,t)$

$Push(b_1,p_1,0) \Rightarrow Empty(p_1,0)$

$Push(b_1,p_1,1) \Rightarrow Empty(p_1,1)$

$Push(b_1,p_1,2) \Rightarrow Empty(p_1,2)$

$\forall b, p, t: Push(b,p,t) \Rightarrow Empty(p,t)$

Actions are sparse

Solver state of $Push(b,p,t)$:
  • unknown: do nothing
  • false: do nothing
  • true: instantiate quantification and ground

Existential Quantifications

$\exists t: \mathit{GoalReached}(t)$

$\mathit{GoalReached}(0) \vee \mathit{GoalReached}(1) \vee \dots$ 
$\exists t[Time]: \mathit{GoalReached}(t)$

Rewrite to: 
$ \mathit{GoalReached} (0) \vee T $
$T \Rightarrow \exists t[\mathit{Time}\setminus\{0\}]: \mathit{GoalReached} (t)$

Solver state of $T$:
  • unknown: do nothing
  • false: do nothing
  • true: rewrite to \[\begin{align*}T &\Rightarrow \mathit{GoalReached} (1) \vee T' \\ &\dots \end{align*}\]

More General

$\forall x: P(x)\Rightarrow \phi(x)$
Delay on $P$:
only instantiate $x$ with values for which $P$ holds

$\exists x: \phi(x)$
only instantiate new values if all previous fail

Lost Propagation

$\forall x: P(x) \Rightarrow \phi(x)$, delayed on $P$
$\phi(1) =\mathbf{f}$

Solution: use two watches
$\forall x: P(x) \land Q(x)\Rightarrow \phi(x)$
Delay on $P$ and $Q$

= generalisation of two watched literal scheme

SoundNESS

Sound if every atom will eventually get a value 

But we can do better!

Construction

= a deterministic recipe to extend 
an interpretation such that
it satisfies certain constraints 

$\forall x: P(x) \Rightarrow \phi(x)$
Default construction: make all $P(d)$'s false

$\forall x: P(x) \Leftrightarrow \phi(x)$
Definitional construction: assign $P(d)$ the value of $\phi(d)$

Constructions

Constructions can be incompatible

Make all P(d)'s true
Assign P(d) the value of Q(d)

Constructions

Constructions can be incompatible with solver state

Make all P(d)'s true
P(1) = false

Lazy Grounding

  • Split theory in 
    • Ground theory Tg
    • High-level (delayed) theory Td
  • For every sentence in Td: 
    • find construction compatible with
      • all other constructions
      • the state of the solver
    • If impossible: ground partially 
      • for relevant instantiations
  • Solver searches model of T g

Lazy Grounding

Afterwards, combine model of Tg   with 
constructions for Td to obtain a model of T

Lazy Grounding (in general)

  • Very general framework
  • Based on definitions and justifications

Definitions

All (inductive) definitions that occur in practice are total:

For every assignment to their parameters,
there is exactly one assignment to the defined 
symbols such that the definition is satisfied

Hence, definitions are constructions

DefinitionS

Grounding of definitions can be delayed on 
all defined symbols:

For a rule $\forall \bar{x}: P(\bar{x})\leftarrow \varphi$:
Delay on $P(\bar{x})$:
  • Unknown: do nothing
  • Otherwise: ground rule 
    • for relevant instantiation

= Dynamic Top-Down Grounding

Implementation

Implemented in $\textrm{IDP}^3$

Experiments

\(\require{color}\) \[ \definecolor{myorange}{RGB}{255,153,0} \newcommand{\fancyprint}[1]{\color{myorange}{#1}} \begin{array}{l|ccc|ccc} benchmark & \textrm{IDP} & \textrm{lazy} & \textrm{ASP} & \textrm{IDP} & \textrm{lazy} & \textrm{ASP}\\ \hline \text{Sokoban} &9 &5 &\fancyprint{10} & 370 &1538 &\fancyprint{22} \\ \text{Disj. Scheduling} &4 &\fancyprint{10} &2 &1933 &\fancyprint{92} &2400 \\ \text{Packing} &9 &\fancyprint{10} &1 &352 &\fancyprint{51} &2704 \\ \text{Labyrinth} &\fancyprint{6} &5 &\fancyprint{6} &1286 &1851 &\fancyprint{1015} \\ \text{Reachability} &1 &\fancyprint{10} &4 &2706 &\fancyprint{7} &1807 \\ \text{St. Marriage} &0 &\fancyprint{10} &5 &3000 &\fancyprint{350} &1563 \\ \text{Graph Colouring} &\fancyprint{7} &3 &4 &\fancyprint{1013} &2103 &1842 \end{array} \]

Related Work

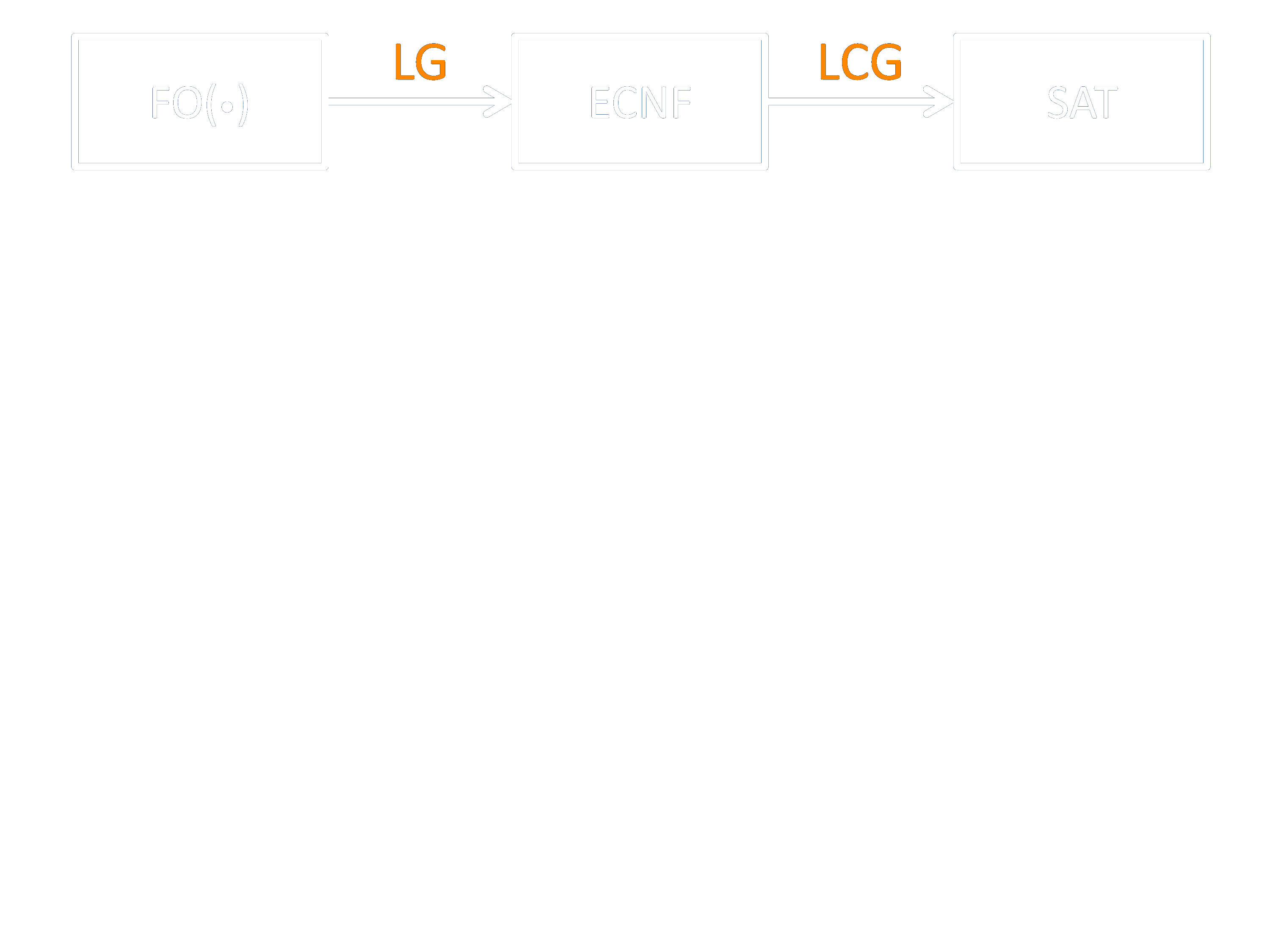
Lazy Clause Generation

  • Fits in lazy grounding framework
  • Richer language
  • Lazy grounding also captures mzn2fzn

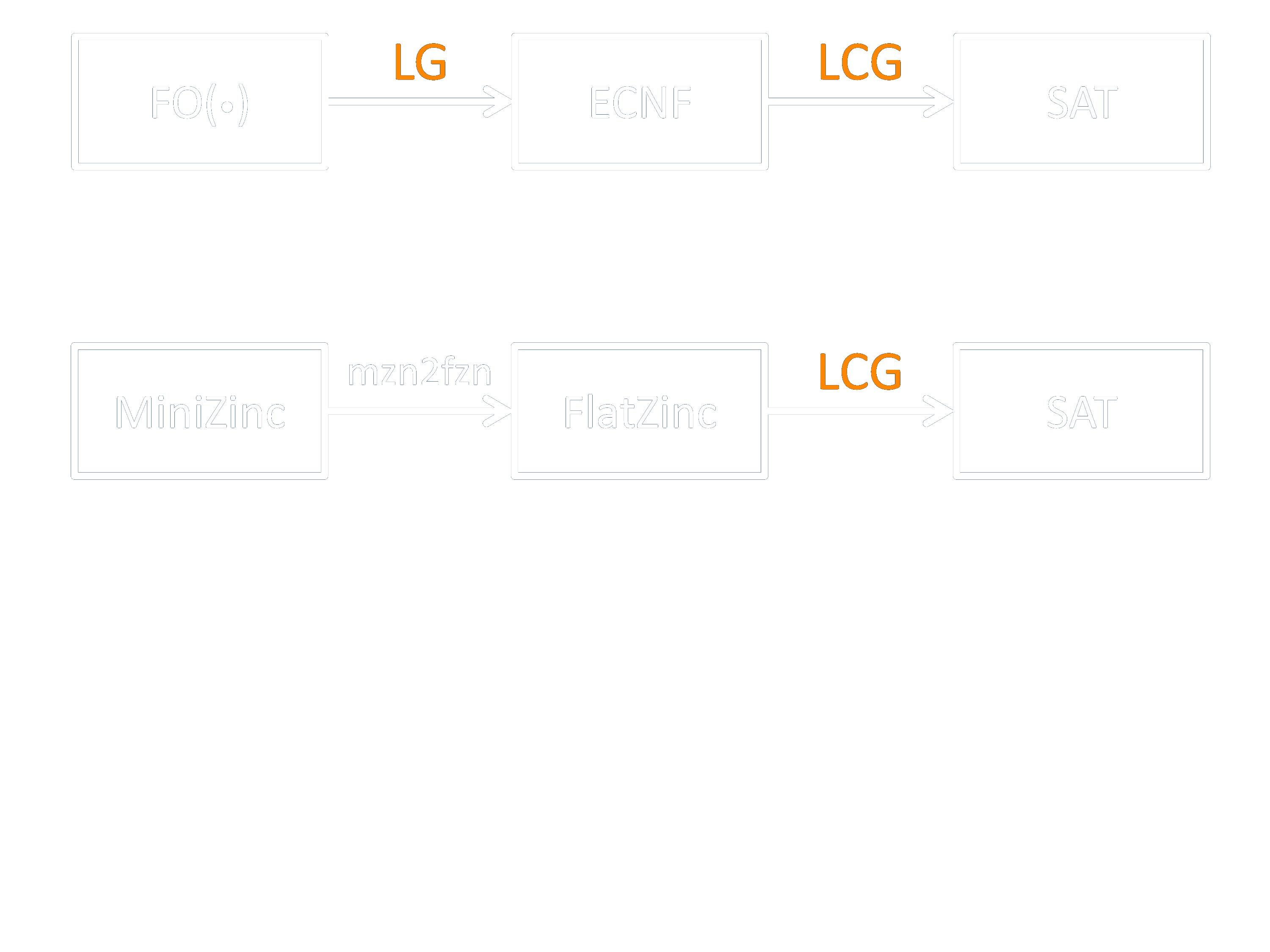
Lazy Clause Generation

  • Fits in lazy grounding framework
  • Richer language
  • Lazy grounding also captures mzn2fzn

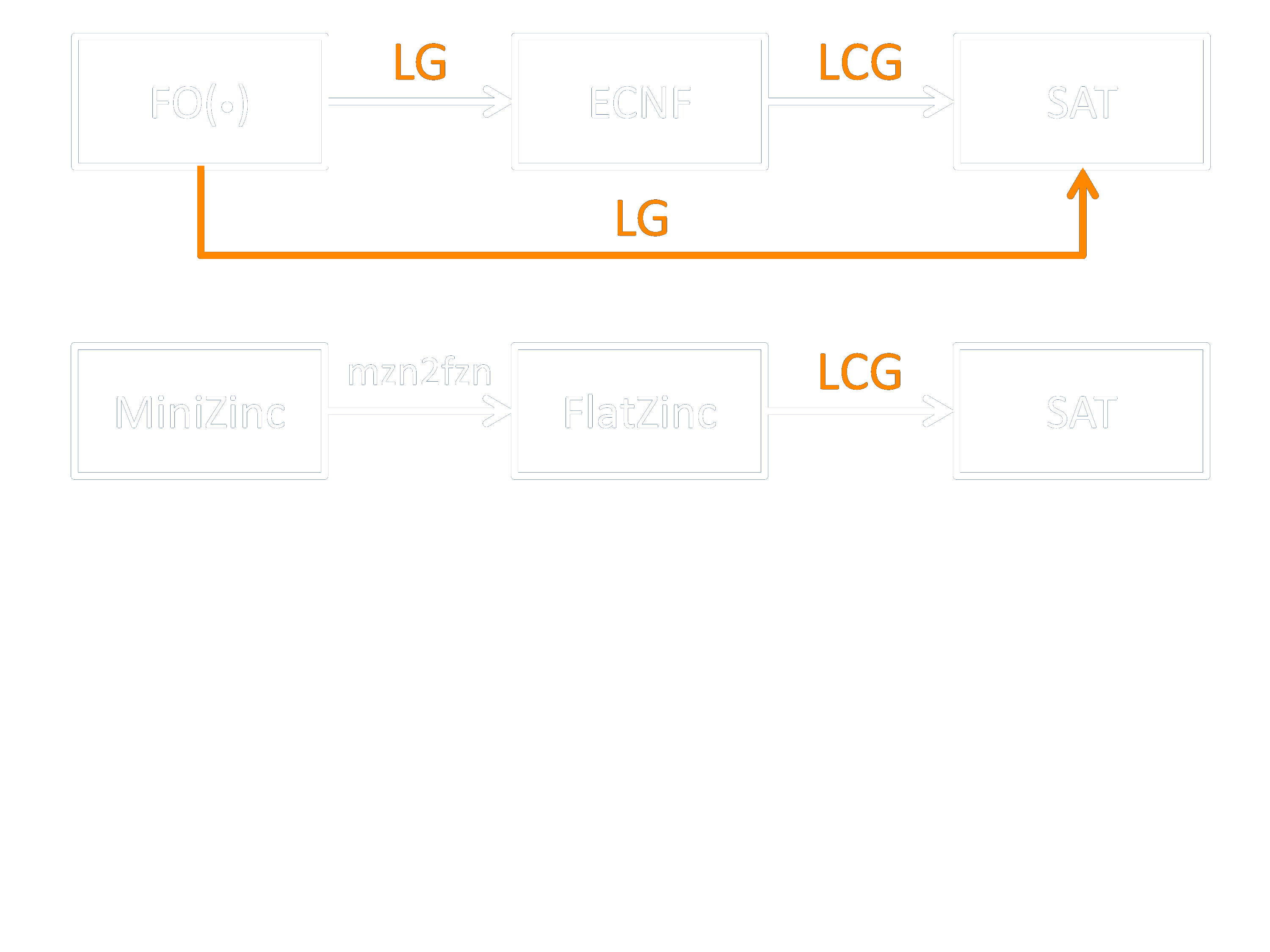
Lazy Clause Generation

  • Fits in lazy grounding framework
  • Richer language
  • Lazy grounding also captures mzn2fzn

LCG, IP and LG

\[A+B=C\]

  • LCG
    • dedicated sum propagator
    • lazily add learned clause, e.g., $A\geq 4 \wedge B\geq 5\Rightarrow C\geq 9$
    • triggers on changes of $A$, $B$ and $C$
  • IP
    • Represent propagations in high level language
    • E.g., whenever (for some $d,d'$) $A\geq d$ and $B\geq d'$, propagate $C\geq d+d'$
    • Automatically obtain propagator
  • LG
    • LG on IP representation ($\forall d, d': A\geq d \wedge B\geq d' \Rightarrow C\geq d+d'$)
    • = LCG behaviour!

Incremental Grounding 

  • special case of lazy grounding

Reference

Broes de Cat, Marc Denecker, Peter J. Stuckey, Maurice Bruynooghe: Lazy Model Expansion: Interleaving Grounding with Search. J. Artif. Intell. Res. (JAIR) 52: 235-286 (2015)